Andrew Alden is a science writer who presented an interesting explanation as to why the continents are the exact shapes required to give the impression that the Earth is expanding. In his blog he proposed that,
"... every continent in the world today has torn edges. Saying it another way, every ocean in the world today arose as a rift in a pre-existing continent. On this, expansionists and plate-tectonicists agree.
However, today there is no oceanic crust that is older than 200 million years. Carey swore that anything older never existed and that there is nothing more to say. Plate tectonics explains that oceanic crust is constantly swept downward into the mantle by subduction. Subduction allows continents to drift, merge and break up indefinitely, a concept taught as the Wilson Cycle. Subduction also allows geologicm history to make sense beyond the last 200 million years. It turns out that there's a lot more to say.
Plate tectonics paints a picture of continental crust constantly rearranging itself. In this scenario, every continent eventually gets all of its edges ripped. In a steady-state Earth like this, you can always interpret the result as an expanding Earth purely from geometry. Every edge, if you go back long enough (200 million years), will find its counterpart. It only looks like the Earth must shrink to accomplish this. It's an optical illusion stemming from a conceptual illusion. ...”
Basically, Andrew Alden is arguing that as the continents moved and crashed into each other they just happened to form the exact shapes required to allow them to fit together on a smaller diameter earth. Here is a concept that we can check because we can work out the probability that the ancient continents would form the exact shapes required to fit together by chance.
Chance is a strange thing. We could break a plate into 30 pieces, throw away 15 (the subducted area) and there must be a remote chance we could reconstruct the remaining 15 as a smaller plate. But most people wouldn't bet on that happening.
This idea of chance presents an interesting query. What is the probability that one continental plate would fit another continental plate purely by chance? The question is really what is the probability that one continental plate will take the shape it has and that is an interesting question.
What is the probability any natural shape will be the exact shape it is? What about a mountain: do we ever see two mountains the same? How about a tree; can we ever find two trees exactly the same shape? What about a rock, river or cloud? Can we ever find any two natural shapes exactly the same?
The probability of finding two shapes in nature that are exactly the same must be vanishing small but the probability can’t be zero. If the universe is infinite then there must be an infinite number of shapes so we can never rule out the possibility of two shapes being identical. Somewhere on the billions of worlds, perhaps in another galaxy, there may be a continent that looks exactly the same shape as Africa.
Nature is completely random and creates many different shapes. This randomness of nature is the same reason those lottery combinations of one, two, three, four, five, six are never seen. Although apparently some people choose them most of us realise that in practice the chance of having exactly those numbers is astonishingly low. So we choose a random set of numbers in the hope that they will be better. But the probability of these random numbers occurring is just the same as the ordered set. For the lottery we can work it out using probability theory. When the lottery draw takes place seven numbers are drawn from the 49, six main balls and one Bonus Ball. To win the jackpot for the game you must match all six numbers in your selection to the six main numbers drawn. Odds of winning the jackpot are almost one in 14 million: and that's just for 6 main numbers. Imagine how much smaller the possibility of one particular shape forming by chance in nature must be.
It’s this very randomness that limits the probability that the continents of the world would fit together by chance so it looks like it has expanded. The lottery combination one, two, three, four, five, six, is heavily ordered just like a particular shape and this is the reason shapes are so different in nature. Everything is formed by chance.
We could say that the probability of achieving one shape is the same as achieving any other shape. Because we can generate particular shapes relatively easily we quite often don’t realise how vastly small the probability of one particular shape being identical to another one is. The whole of nature is full of irregularly shaped features. The probability that one continental shape would be one particular shape is exactly the same probability as forming a perfect pattern in nature. Perhaps a perfect line or a perfect circle. Can we ever imagine a continent that had a perfectly straight coastline stretching for thousands of miles? Or perhaps one that was perfectly round? The laws of probability make no distinction between these shapes and the shapes they are. It’s all the same probability just like the lottery. This is how small the probability of one coast fitting another by chance actually is in practice.
As a test you might like to rip a map up into 30 random shapes. Now choose 15 pieces at random from the ocean to represent the area that will be subducted and throw these away. If Andrew Alden is correct you should be able to reconstruct all the remaining pieces so they all fit perfectly together. I don’t believe they will. You can even cheat and produce various odd shapes with scissors (something we never see in nature) and they will still not fit together.
What exactly is the probability of all the continents forming the exact shapes required by chance? In my book I suggested the very conservative estimate of less than one in a million chance but it must be much smaller than this. We can relatively easily work out the probability of one simple shape forming exactly the same shape as another so they fit together. Look at the shape of the line below with a randomly generated shape of line attempting to match it by chance.
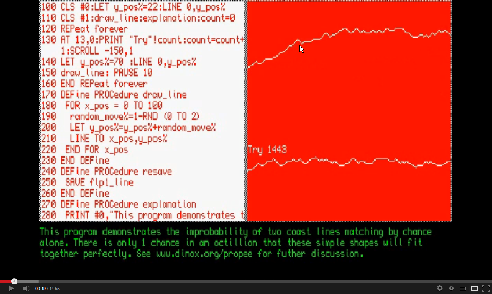Each line comprises only 100 selected points. The second point on the randomly generated line can move up or down so there are 21 (2) possible line shapes that can be produced with just these two points. The next point can also move up or down so there are now 22 (4) possible lines shapes. The number of possible line shapes increases exponentially with each new point: 23 (8), 24 (16), 25 (32), 26 (64), 27 (128), 26 (256), and so on. Once we reach 100 points there are 299 possible line shapes. Each random shape has one chance in 6.3 x 1029 of matching. Or to put another way it's less than one chance in 630 billion, billion, billion. It's an astonishingly low chance for just a simple line with only 100 points.
My original estimate for the Expanding Earth forming by chance alone was massively conservative. It isn’t less than one chance in a million, or billion, or even a trillion. It’s less than one chance in an octillion: a number so large I needed to look up its name. Now consider that the real Earth has multiple coastlines which all need to fit together. The probability of this happening by chance is so small it is virtually impossible.
We never see geometric shapes in nature because the probability of this happening is so astronomically small that we would be astounded if we did see it. We never see a straight river, or a perfectly circular puddle or a pyramid shaped mountain but all these are just as likely to form as any other shape. Having one unique shape is vanishingly small in nature. This is why I can't believe Andrew Alden's explanation that the continents drifted around, while some ocean floor was destroyed by subduction, and this formed exactly the shapes required to allow them to be reconstructed on a smaller ancient Earth. In practice the probably is so small it can only be explained by an Expanding Earth.
Further Reading
- The Expanding Earth Animation: Why It Is Really a Plate-Tectonic Animation by Andrew Alden. Full article (wayback) here
- Probability theory on Wikipedia here
Comment on Facebook, Twitter, YouTube, LinkedIn or Contact me
Page Updated 12 Oct 2026
Wayback
Comments
@janpeterdejong on YouTube - This is the reason why I always say that the perfect fits on a smaller globe should not be denied and are not a coincidence! Not a very exciting video but for those that follow the discussion on expanding earth theory it is quite clear what is means to say.
Felix Lanzalaco on Facebook - any maths references for this. a statistical model is the strongest approach to take.
Palaeogravity Laboratory - dinox.org - Yes, I agree. I think both of us think that any sort of mathematical analysis must provide one of the strongest proofs for EE (or not). One geologist friend pointed out some time ago that this may not seem as convincing as we believe to a geologist since all geologists already know the Earth is unique. No other planet has subduction for example. So it’s only a small step to dismiss the argument that there is only 1 chance in an octillion of it forming by any other process than on an Expanding Earth. I found this to be an interesting point of view.
N.B. My original discussion with him was about a probability of 1 in a million since I hadn’t done this calculation then. I’ll have to raise the point again when I see him to see if he thinks a reduced probability makes any difference. After all, as the probability becomes less it becomes more and more impossible.
Felix Lanzalaco on Facebook - Comparing it to another system is off topic. Doesnt matter how the system arises.. to calculate plate fitback is a pure geometrical probability argument that stands on its own right.
there ends up two probability statistics...
1. The EE probability is that of whether its geometric probable to fit as it does.. Stat 1
The detail of the plate edges becomes part of each plate. The space between the plates is the probability space we are trying to calculate, against the ocean age map.
2. Then with that model restrict the plate movement to the isochron age windback ... Stat 2
i.e. The statistical regression test is the probability of the plates not being able to regress back (or forward) along the isochron age line. I dont see what difference the direction back or forward in time makes because its math not physics here. A nice clear way to do it, is take the animation like adams or maxlow etc.. then push the statistical analysis along by 1Ma.. have all the stats on one side of the animation, so we can see the probability increase with time. This is another important mathematical point. IF the probability keeps compounding its unlikliehood in an exponential manner as each Ma passes.. Then we end up with a sum of probabilities that is linear in nature.
But first problem is all the isochron data needs reviewed...Don findlay says he thinks there is a lot of problems with that ocean floor map, but it wasnt clear if its enough to throw the whole lot out or not.
Felix Lanzalaco on Facebook - Another aspect is, that the continent plates are already sharply defined to some agreed resolution, so we can leave calculus (i.e the integrals which derived smooth motion paths out of it..the colour bands on the floor). The statistics will smooth out the information anyway, so we dont want to compound smoothed data.. Everything is sharp already, the discrete units of time, the resolution of the model (plates).
I will see if don findlay is on FB.. he has some opinions about how the floor map was constructed. What is key to find is how much smoothing has been extrapolated from the shipping lanes... it would be good to get the original data even without the smoothing. Then almost every bit of data is sharp and independent of each other...
Maybe this is not clear, using smoothed data can start such a project on a house of cards...so you start with as much sharp and independent data as possible
Stephen Hurrell on Facebook - Yes you are correct; the ocean floor data has been simplified to 5 Ma increments. The only place I’ve seen the raw data published is in Dr Hugh Owen’s book “Atlas of Continental Displacement, 200 Million Years to the Present”. That’s old now so I don’t know where you might get newer raw data from. If you think Hugh Owen’s data might be useful I could probably scan the relevant pages in for you. Details of the book are here:
P.S. Hugh Owen shared a lot of his data here
Share this page